Contributions
- FSQ can serve as a replacement for VQ in various architectures, for different datasets and tasks. There is a reduction of only $0.5 - 3\%$ in the respective metrics, and FSQ correspondingly get highlty similar visual results.
- FSQ is able to leverage large codebooks for better reconstruction metrics, and better sample quality. The codebook usage is very high for FSQ ($\approx100\%$ for most models), without relying on any auxiliary losses. Besides, the dimension of FSQ is much smaller than VQ (typically d < 10 for FSQ, but d ≥ 512 for VQ).
Method
-
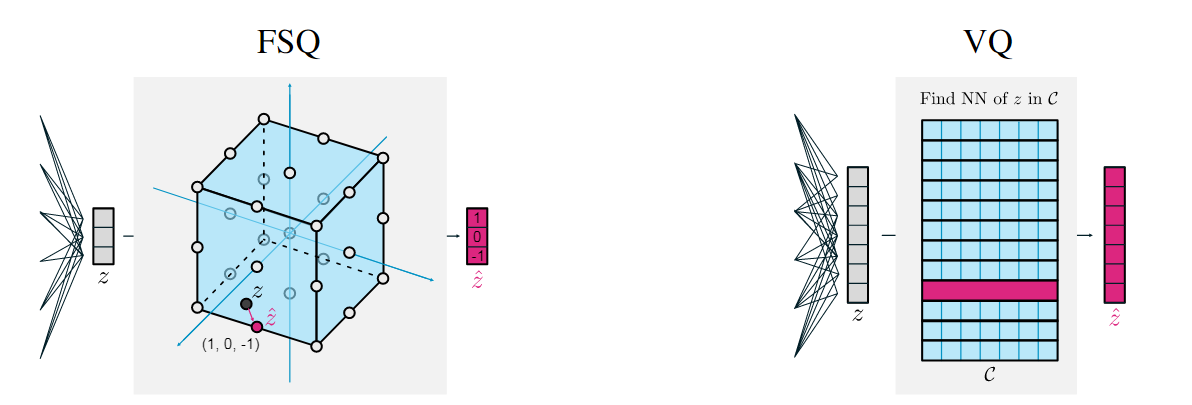
In the high-level intuition, VQ defines a learnable Voronoi partition in the highdimensional latent space. FSQ, by contrast, relies on a simple, fixed grid partition in a much lower-dimensional space. Because VAEs have a relatively high model capacity, and thus the non-linearity of VQ can be “absorbed” into encoder and decoder, so that FSQ enables partitions of the VAE input space of similar complexity as VQ.
-
Given a $d$-dimensional representation $z\in \mathbb R^d$, author first applies a bounding function $f$ (e.g., $f:z\to ⌊L/2⌋tanh(z)$), and then round them to integers $\hat z=round(f(z))$. Each channel/entry will take one of $L$ unique values. Thereby, we have $\hat z\in C$, where $C$ is the implied codebook, given by the product of these per-channel codebook sets, with $| c|=L^d$. The vectors in $C$ can simply be enumerated leading to a bijection from any $\hat z$ to an integer in $\{1,…,L^d\}$. Therefore, VQ can be replaced with FSQ in any neural network-related setup where VQ is commonly used.