Contribution
- Using CNNS to learn a context-rich vocabulary of image constituents.
- Utilizing transformers to efficiently model their composition within high-resolution images.
Learning an Effective Codebook of Image Constituents
-
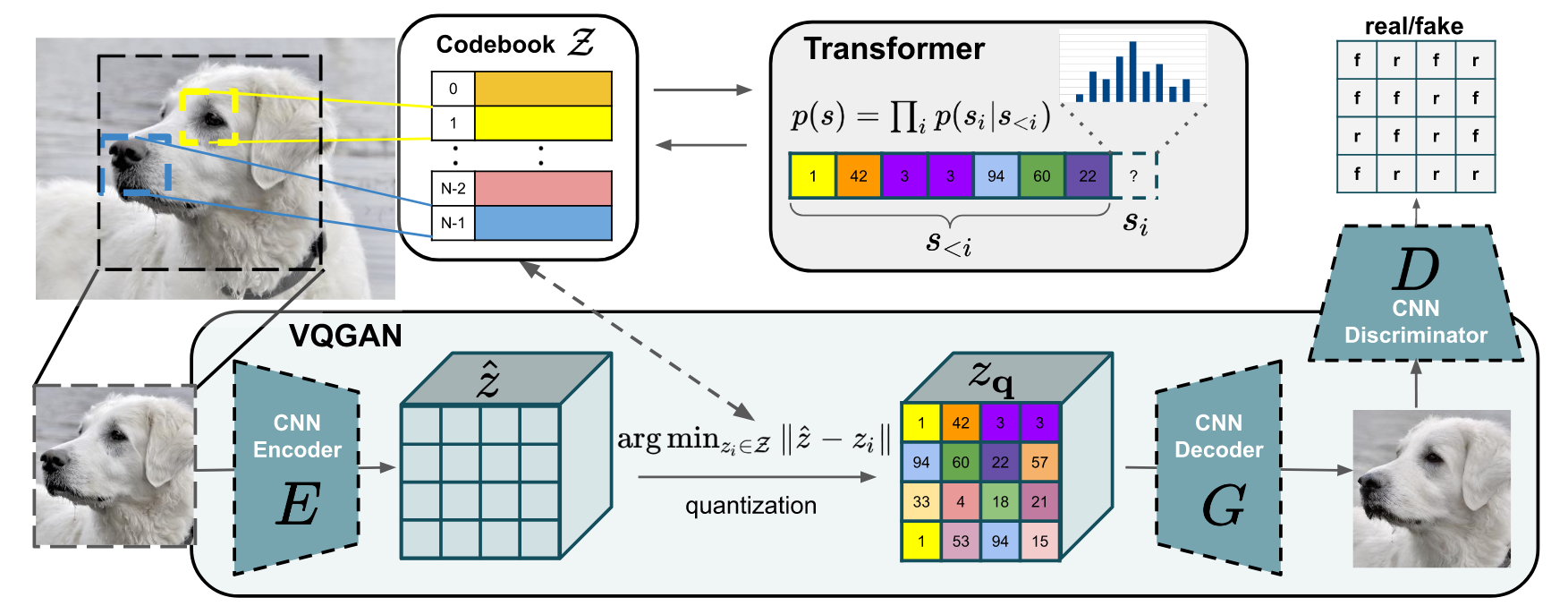
Standard process of VQ-VAE. Image $x\in \mathbb R^{H\times W\times 3}$ can be represented by a spatial collection of codebook entries $z_q\in \mathbb R^{h\times w\times n_z}$, where $n_z$ is the dimensionality of codes. The author learn a convolutional model consisting of encoder $E$ and a decoder $G$, such that taken together, they learn to represent images with codes from a learned, discrete codebook $\mathcal Z=\{z_k\}^K_{k=1} \subset \mathbb R^{n_z}$.
-
Step1. Using the encoder $E$ to get the embedding $\hat z=E(x)\in \mathbb R^{h\times w\times n_z}$.
-
Step2. Using the subsequent element-wise quantization $q(\cdot)$ of each spatial code $\hat z_{i,j}\in \mathbb R^{n_z}$ onto its closest codebook entry $z_k$:
\[z_q=q(\hat z):= \left(\mathop{\arg\min}\limits_{z_k\in \mathcal Z}\|\hat z_{i,j}-z_k\|\right)\in \mathbb R^{h\times w\times n_z}\] -
Step3. Approximating the image by $\hat x=G(z_q)$ by decoder $G$.
The reconstruction $\hat x \approx x$ is given by
\[\hat x=G(z_q)=G(q(E(x)))\]Backpropagation through the non-differentiable quantization operation is achieved by a straight-through gradient estimator, which simply copies the gradients from the decoder to the encoder, such that the model and codebook can be trained end-to-end via the loss function
\[\mathcal L_{VQ}(E,G,\mathcal Z)=\|x-\hat x\|^2+\|sg[E(x)]-z_q\|^2_2+\|sg[z_q]-E(x)\|^2_2\]Here, $\mathcal L_{rec}(E,G,\mathcal Z)=\|x-\hat x\|^2$ is a reconstruction loss, $sg[\cdot]$ denotes the stop-gradient operation, and $\|sg[z_q]-E(x)\|^2_2$ is the socalled “commitment loss”.
-
-
Learning a Perceptually Rich Codebook. Author uses a discriminator and perceptual loss to keep good perceptual quality at increased compression rate. More specifically, author replace the $L_2$ loss used in VQ-VAE for $\mathcal L_{rec}$ by a perceptual loss and introduce an adversarial training procedure with a patch-based discriminator $D$ that aims to differentiate between real and reconstructed images.
\[\mathcal L_{GAN}(\{E,G,\mathcal Z\}, D)=[logD(x)+log(1-D(\hat x))]\]The complete objective for finding the optimal compression model $\mathcal Q^=\{E^,G^,\mathcal Z^\}$ then reads
\[\mathcal Q^*=\mathop{\arg\min}\limits_{E,G,\mathcal Z}\mathop{\max}\limits_D \mathbb E_{x\sim p(x)}\left[\mathcal L_{VQ}(E,G,\mathcal Z)+\lambda \mathcal L_{GAN}(\{E,G,\mathcal Z\},D)\right]\]where we compute the adaptive weight $\lambda$ according to
\[\lambda =\frac{\nabla_{G_L}[\mathcal L_{rec}]}{\nabla_{G_L}[\mathcal L_{GAN}]+\delta}\]where $\mathcal L_{rec}$ is the perceptual reconstruction loss, $\nabla_{G_L}[\cdot]$ denotes the gradient of its input w.r.t. the last layer $L$ of the decoder.
Learning the Composition of Images with Transformers
-
Latent Transformers. With $E$ and $G$ available, we can now represent images in terms of the codenook-indices of their encodings. More precisely, the quantized encoding of an image $x$ is given by $z_q=q(E(x)) \in \mathbb R^{x\times w\times n_z}$ and is equivalent to a sequence $s\in \{0, \cdots,|\mathcal Z|-1\}^{h\times w}$ of indices from the codebook, which is obtained by replacing each code by its index in the codebook $\mathcal Z$:
\[s_{i,j}=k \text{ such that } (z_q)_{ij}=z_k\]By mapping indices of a sequence $s$ back to their corresponding codebook entries, $z_q=\left(z_{s_{ij}}\right)$ is readily recovered and decoded to an image $\hat x=G(z_q)$.
Thus, after choosing some ordering of the indices in $s$, image-generation can be formulated as autoregressive next-index prediction: Given indices $s_{<i}$, the transformer learns to predict the distribution of possible next indices.
-
Conditioned Synthesis. If the image synthesis task use the additional information $c$ to guide the generation process, the task is then to learn the likelihood of the sequence given this information:
\[p(s|c)=\prod_ip(s_i|s_{<i}, c)\]If the conditioning information $c$ has spatial extent, we can learn another VQGAN to obtain again an index-based representation $r\in \{0,\cdots,|\mathcal Z_c|-1\}^{h_c\times w_c}$ with the newly obtained codebook $\mathcal Z_c$. And we can use the prepend $r$ and $s$ to restrict the output of the transformer.